The word tessellation originates from the ancient Greek word tessares, meaning four or four-cornered. The Latin word tessera means cube or die and tessella refers to small squares laid in a mosaic. From these ancient words derive similar terms in various practical applications.
In mathematics, tessellation refers to the study of “tiling” or how regular shapes can be placed to fill an infinite space with no gaps and no overlapping shapes. This is a mathematical discipline which has been evolving since the early 17th century and formally recognized in the 19th century.
Types of Tessellations
Tessellations can be divided into several categories; sample subsets include the following:
-
- Regular Tessellations
Regular tessellations form patterns consisting of a single shape. Only three types of regular tessellations exist: triangles, squares, and hexagons. These shapes by themselves can fill a surface because their interior angles are exact divisors of 360°. Of these shapes, only the squares line up with one another without requiring rotating or shifting.
- Regular Tessellations
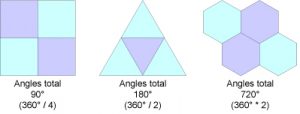
Figure 1: Tessellations using one type of polygon.
-
- Semi-Regular Tessellations
Semi-regular tessellations combine two types of polygons that share a common vertice. For example, a regular hexagon with a 1″ side can line up with a 1″ square. Nine types of semi-regular tessellations exist.
- Semi-Regular Tessellations
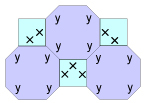
Figure 2. Tessellations using two types of polygons.
- Replicating Shapes (Rep-Tiles)
Rep-tiles consist of congruent shapes that are rotated to create ever-larger versions of the shaped in an infinite series. Often called polyforms, rep-tiles are implicit in such phenomena as the classic illustration of the Golden Mean and the Penrose Tile. - 3D Tessellations
Tessellations can take 3 dimensional forms as in truncated octahedrons and in geodesic domes. Such forms can combine combinations of shapes; only five are regular polyhedra (i.e. platonic) shapes. - Non-Periodic Tessellations
Non-periodic (aperiodic) tilings have no regular, repetitious patterns but rather evolve as they expand over a plane. The Dutch artist M.C. Escher produced well-known examples of such tilings, such as his graphic of birds that morph into triangles.
Practical Applications of Tessellations
Tessellations have practical applications in many realms, from art and architecture to science, technology, and production.
In design and architecture, tessellation refers to the paving of walls, floors, or other surfaces with a pattern of small tiles (tesserae) made of ceramics, glass, metal leaf, stone, or other materials. These tesserae normally are cut into geometric shapes that fit together perfectly in either simple or complex designs in a seemingly infinite pattern while providing continuous surface coverage. This is an ancient technique that you can see in buildings and wall murals in Greece, Italy, Turkey, India, and many other countries. Tessellations are particularly prominent in Islamic art, which forbids representational images of God; therefore, its designs favor abstract forms with mathematical underpinnings.
Although tesserae often consist of abstract shapes, primarily symmetrical rectangles, hexagons, octagons, and other polygons, they also can consist of figurative elements, as in the work of artists like Kolomon Moser (1868-1918) and M.C. Escher (1898-1972). Escher is famed for his tessellations composed of horses, butterflies, birds, and imaginary creatures (which in the 1990s formed the basis of a popular line of upholstery fabrics!). Many of his designs “morph” different shapes, such as hexagons evolving into creatures.
Many contemporary artists apply tessellations in their work. These designs, which can contain representational elements, are often called diaper designs.
Although often considered an art or design application, tessellations can be found in nature, as in the patterns of snowflakes, honeycombs, and cracks in dry earth. Scientists have determined that beehives are composed of hexagons because that is the most efficient way for bees to construct their homes.
Tessellations appear in various scientific and engineering disciplines. Chemical discoveries show that certain carbon molecules take the shape of a truncated isocahedren. Geodesic domes are both theoretical 3D geometric constructs and built structures.
